The supposedly missing dark energy of the cosmos is found quantitatively in a direct analysis without involving ordinary energy. The analysis relies on five dimensional Kaluza-Klein spacetime and a Lagrangian constrained by an auxiliary condition. Employing the Lagrangian multiplier method, it is found that this multiplier is equal to the dark energy of the cosmos and is given by  where E is energy, m is mass, c is the speed of light,
where E is energy, m is mass, c is the speed of light,  and λ is the Lagrangian multiplier. The result is in full agreement with cosmic measurements which were awarded the 2011 Nobel Prize in Physics as well as with the interpretation that dark energy is the energy of the quantum wave while ordinary energy is the energy of the quantum particle. Consequently dark energy could not be found directly using our current measurement methods because measurement leads to wave collapse leaving only the quantum particle and its ordinary energy intact.
and λ is the Lagrangian multiplier. The result is in full agreement with cosmic measurements which were awarded the 2011 Nobel Prize in Physics as well as with the interpretation that dark energy is the energy of the quantum wave while ordinary energy is the energy of the quantum particle. Consequently dark energy could not be found directly using our current measurement methods because measurement leads to wave collapse leaving only the quantum particle and its ordinary energy intact.
Dark Energy Introduction
Monday, August 26, 2013
What Is the Missing Dark Energy in a Nutshell and the Hawking-Hartle Quantum Wave Collapse
We reason that in quantum cosmology there are two kinds of energy. The first is the ordinary energy of the quantum particle which we can measure. The second is the dark energy of the quantum wave by quantum duality. Because measurement collapses the Hawking-Hartle quantum wave of the cosmos, dark energy cannot be detected or measured in any conventional manner. The quantitative results are confirmed using some exact solutions for the hydrogen atom. In particular the ordinary energy of the quantum particle is given by E(0) = ( /2)(mc2) where
/2)(mc2) where  is Hardy’s probability of quantum entanglement,
is Hardy’s probability of quantum entanglement,  =(
=( - 1)/2 is the Hausdorff dimension of the zero measure thin Cantor set modeling the quantum particle, while the dark energy of the quantum wave is given by E(D) = (5
- 1)/2 is the Hausdorff dimension of the zero measure thin Cantor set modeling the quantum particle, while the dark energy of the quantum wave is given by E(D) = (5 /2)(mc2) where
/2)(mc2) where  is the Hausdorff dimension of the positive measure thick empty Cantor set modeling the quantum wave and the factor five (5) is the Kaluza-Klein spacetime dimension to which the measure zero thin Cantor set D(0) = (0,
is the Hausdorff dimension of the positive measure thick empty Cantor set modeling the quantum wave and the factor five (5) is the Kaluza-Klein spacetime dimension to which the measure zero thin Cantor set D(0) = (0, ) and the thick empty setD(-1) = (1,
) and the thick empty setD(-1) = (1, ) must be lifted to give the five dimensional analogue sets namely
) must be lifted to give the five dimensional analogue sets namely  and 5
and 5 needed for calculating the energy density E(0) and E(D) which together add to Einstein’s maximal total energy densityE(total) = E(0) + E(D) = mc2 = E(Einstein). These results seem to be in complete agreement with the WMAP, supernova and recent Planck cosmic measurement as well as the 2005 quantum gravity experiments of V.V. Nesvizhersky and his associates. It also confirms the equivalence of wormhole solutions of Einstein’s equations and quantum entanglement by scaling the Planck scale.
needed for calculating the energy density E(0) and E(D) which together add to Einstein’s maximal total energy densityE(total) = E(0) + E(D) = mc2 = E(Einstein). These results seem to be in complete agreement with the WMAP, supernova and recent Planck cosmic measurement as well as the 2005 quantum gravity experiments of V.V. Nesvizhersky and his associates. It also confirms the equivalence of wormhole solutions of Einstein’s equations and quantum entanglement by scaling the Planck scale.
 /2)(mc2) where
/2)(mc2) where  is Hardy’s probability of quantum entanglement,
is Hardy’s probability of quantum entanglement,  =(
=( - 1)/2 is the Hausdorff dimension of the zero measure thin Cantor set modeling the quantum particle, while the dark energy of the quantum wave is given by E(D) = (5
- 1)/2 is the Hausdorff dimension of the zero measure thin Cantor set modeling the quantum particle, while the dark energy of the quantum wave is given by E(D) = (5 /2)(mc2) where
/2)(mc2) where  is the Hausdorff dimension of the positive measure thick empty Cantor set modeling the quantum wave and the factor five (5) is the Kaluza-Klein spacetime dimension to which the measure zero thin Cantor set D(0) = (0,
is the Hausdorff dimension of the positive measure thick empty Cantor set modeling the quantum wave and the factor five (5) is the Kaluza-Klein spacetime dimension to which the measure zero thin Cantor set D(0) = (0, ) and the thick empty setD(-1) = (1,
) and the thick empty setD(-1) = (1, ) must be lifted to give the five dimensional analogue sets namely
) must be lifted to give the five dimensional analogue sets namely  and 5
and 5 needed for calculating the energy density E(0) and E(D) which together add to Einstein’s maximal total energy densityE(total) = E(0) + E(D) = mc2 = E(Einstein). These results seem to be in complete agreement with the WMAP, supernova and recent Planck cosmic measurement as well as the 2005 quantum gravity experiments of V.V. Nesvizhersky and his associates. It also confirms the equivalence of wormhole solutions of Einstein’s equations and quantum entanglement by scaling the Planck scale.
needed for calculating the energy density E(0) and E(D) which together add to Einstein’s maximal total energy densityE(total) = E(0) + E(D) = mc2 = E(Einstein). These results seem to be in complete agreement with the WMAP, supernova and recent Planck cosmic measurement as well as the 2005 quantum gravity experiments of V.V. Nesvizhersky and his associates. It also confirms the equivalence of wormhole solutions of Einstein’s equations and quantum entanglement by scaling the Planck scale.The Missing Dark Energy of the Cosmos from Light Cone Topological Velocity and Scaling of the Planck Scale
The paper presents an exact analysis leading to an accurate theoretical prediction of the amount of the mysteriously missing hypothetical dark energy density in the cosmos. The value found, namely 95.4915028% is in full agreement with earlier analysis, the WMAP and the supernova cosmic measurements. The work follows first the strategy of finding a critical point which separates a semi-classical regime from a fully relativistic domain given by topological unit interval velocity parameter then proceeds to wider aspects of a topological quantum field of fractal unit interval. This idea of a critical velocity parameter was first advanced by Sigalotti and Mejias in 2006 who proposed a critical value equal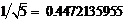 . A second interesting proposal made in 2012 by Hendi and Sharifzadeh set the critical point at 0.8256645. The present analysis is based upon a light cone velocity quantized coordinate. This leads to the same quantum relativity energy mass relation found in earlier publications by rescaling that of Einstein’s special relativity. Two effective quantum gravity formulae are obtained. The first is for the ordinary measurable energy of the quantum particle
. A second interesting proposal made in 2012 by Hendi and Sharifzadeh set the critical point at 0.8256645. The present analysis is based upon a light cone velocity quantized coordinate. This leads to the same quantum relativity energy mass relation found in earlier publications by rescaling that of Einstein’s special relativity. Two effective quantum gravity formulae are obtained. The first is for the ordinary measurable energy of the quantum particle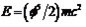 while the second is for dark energy density of the quantum wave which we cannot measure directly and we can only infer its existence from the measured accelerated expansion of the universe E(D) =
while the second is for dark energy density of the quantum wave which we cannot measure directly and we can only infer its existence from the measured accelerated expansion of the universe E(D) = 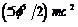 where
where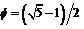 . The critical velocity parameter in this case arises naturally to be
. The critical velocity parameter in this case arises naturally to be 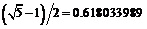 . The results so obtained are validated using a heuristic Lorentzian transformation. Finally the entire methodology is put into the wider perspective of a fundamental scaling theory for the Planck scale proposed by G. Gross.
. The results so obtained are validated using a heuristic Lorentzian transformation. Finally the entire methodology is put into the wider perspective of a fundamental scaling theory for the Planck scale proposed by G. Gross.
To continue reading the paper please downloads it from here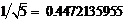 . A second interesting proposal made in 2012 by Hendi and Sharifzadeh set the critical point at 0.8256645. The present analysis is based upon a light cone velocity quantized coordinate. This leads to the same quantum relativity energy mass relation found in earlier publications by rescaling that of Einstein’s special relativity. Two effective quantum gravity formulae are obtained. The first is for the ordinary measurable energy of the quantum particle
. A second interesting proposal made in 2012 by Hendi and Sharifzadeh set the critical point at 0.8256645. The present analysis is based upon a light cone velocity quantized coordinate. This leads to the same quantum relativity energy mass relation found in earlier publications by rescaling that of Einstein’s special relativity. Two effective quantum gravity formulae are obtained. The first is for the ordinary measurable energy of the quantum particle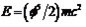 while the second is for dark energy density of the quantum wave which we cannot measure directly and we can only infer its existence from the measured accelerated expansion of the universe E(D) =
while the second is for dark energy density of the quantum wave which we cannot measure directly and we can only infer its existence from the measured accelerated expansion of the universe E(D) = 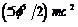 where
where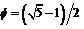 . The critical velocity parameter in this case arises naturally to be
. The critical velocity parameter in this case arises naturally to be 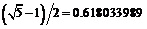 . The results so obtained are validated using a heuristic Lorentzian transformation. Finally the entire methodology is put into the wider perspective of a fundamental scaling theory for the Planck scale proposed by G. Gross.
. The results so obtained are validated using a heuristic Lorentzian transformation. Finally the entire methodology is put into the wider perspective of a fundamental scaling theory for the Planck scale proposed by G. Gross.
Subscribe to:
Comments (Atom)









